Calculating compound growth in JavaScript

A couple of days ago, I sat around the computer and browsing the internet like any other day. I came across this cool website called omni calculator and tried out a couple of their calculators. Since my pretty large interest in finance, I found that they had a tool for calculating the Compound growth and adding a lot of cool parameters to it. And I know for sure, that there are a lot of people having blogs and websites related to economics and so on, so I thought I create some function and write about it - and hopefully, someone will find it and maybe even get inspired to use it.

Compound growth - The algorithm

The algorithm is fairly simple, it looks like this.

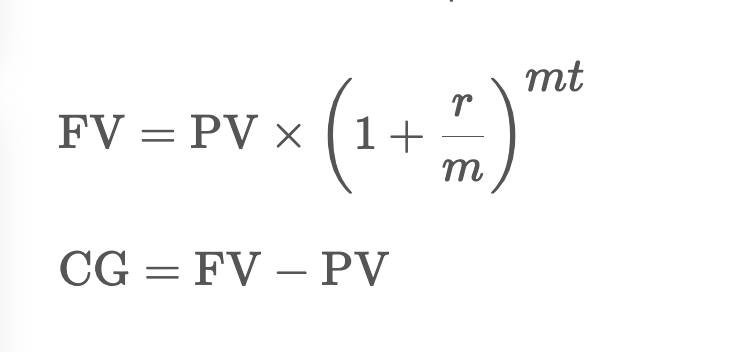
Image was taken from omni compound growth calculator

• PV - Initial balance or present value
• r – Annual interest rate
• m – Number of times the interest is compounded per year (compounding frequency)
• t – Number of years
• FV – Future value of the initial balance
• CG – Compound growth

Let's do it in code

function compoundGrowth(pv, r, t, m = 1) {
  const fv = pv * (1 + r / 100 / m) ** (m * t);
  const cg = fv - pv;

  return {
    finalValue: Number(fv).toFixed(2),
    compoundGrowth: Number(cg).toFixed(2),
  };
}

All right. There we have it. Let's do some tests on it..

• 1k starting value, 5 percent interest rate, 25 years
• 10k starting value, 10 percent interest rate, 10 years
• 100k starting value, 8 percent interest rate, 5 years

compoundGrowth(1000, 5, 25); // finalValue: 3386.35, compoundGrowth: 2386.35
compoundGrowth(10000, 10, 10); // finalValue: 25937.42, compoundGrowth: 15937.42
compoundGrowth(100000, 8, 5); // finalValue: 146932.81, compoundGrowth: 46932.81

Compound growth with monthly deposits

Now we will take into account, that a person can add their monthly deposits as well.

function compoundGrowthWithDeposit(initial, interest, years, monthlyDeposit) {
  const allYears = [];
  for (let i = 0; i < years; i++) {
    // Our "initial" value is our last year total savings, first time, it is our starting value
    const prevInitValue = i > 0 ? allYears[i - 1].finalValue : initial;
    // All months deposits for a year
    const totalSavings = monthlyDeposit * 12;
    // Calculating one years compound growth with our total savings + our final value from last year
    // We also adding our totally saved amount in the object
    allYears.push({
      ...compoundGrowth(prevInitValue + totalSavings, interest, 1, 1),
      saved: monthlyDeposit * 12 + (allYears[i - 1]?.saved ?? 0),
    });
  }

// Returning three values. totalCompound, this is our total amount of "earned" money by the interest rate
// totalSaved is our total amount of saved money
// finalValue, this is the result of all years of both savings and compound growth
return {
    totalCompound: allYears.reduce(
      (accumulator, currentValue) =>
        (accumulator += Number(currentValue.compoundGrowth)),
      0
    ),
    totalSaved: monthlyDeposit * 12 * years,
    finalValue: allYears[allYears.length - 1].finalValue,
  };
}

Let's give it a go. We will try the same examples from above, but with a monthly deposit of $500.

Result

compoundGrowthWithDeposit(1000, 5, 25, 500);
// { totalCompound: 16704.62, totalSaved: 150000, finalValue: '23704.76' }
compoundGrowthWithDeposit(10000, 10, 10, 500);
// { totalCompound: 25499.91, totalSaved: 60000, finalValue: '41499.99' }
compoundGrowthWithDeposit(100000, 8, 5, 500);
// { totalCompound: 49748.78, totalSaved: 30000, finalValue: '155748.82' }

Outro

In this article, we created two algorithms for calculating the compound growth. One for only interest effects and one which takes montly deposits into account as well. There is however room for making our last algorithm a little bit more sophisticated where we could for example make the monthly deposit grow each year by a certain amount or percent, or where we could make the amount of compounds be more than just 1 per year. But this function will give a good hint of how much money will grow. I tried to compare it with other online calculators and it is matching the results quite all right I would say. Depending on the different parameters the online tools are using, they all show slightly different results.

I hope you found this article interesting. Thanks for reading!